2. 油藏数值模拟方程的求解#

2.1. 求解流动方程#

上面得到的流动方程描述了整个系统——油藏模型——中的全部状态。任何一个点中的流动都可以用上述的方程来求解。但是在实际解决问题的时候，我们不可能对整个油藏中所有的点都求解。求解上述方程的技术已经在各行业都有应用了，这里我们不再介绍全部的研究过程，读者如果有兴趣可以参考相关文献资料。

2.1.1. 建立离散化网格系统#

既然我们不是要求解所有的点，那么就可以引入离散化网格系统。把连续的真实物体近似为一系列离散的网格所组成的网格系统。一维问题可以选择线状排列的网格系统，二维问题可以选择以问题所在面排列的网格系统，三维问题可以选择问题所在空间的中排列的三维网格系统。那么前面提出的岩芯模型分别考虑为一维、二维、三维问题下所建立的离散化网格系统，如下图所示：

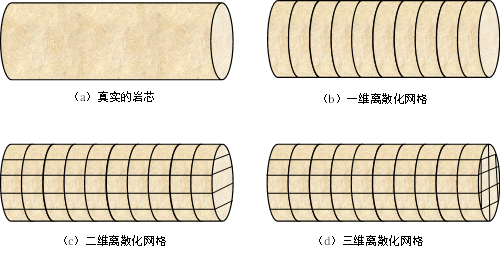
_images/rs006.png

上图中是把原来的岩芯按照不同的方向“切”成了小块，每一小块就是一个网格。由于岩芯是圆柱体，所以“切”出的小块有曲面组成。在理论推导中，如果网格的形状有曲线或者弧面的表示会增加问题求解的难度，因此在处理网格时，都会选择直线和平面的网格形状，离散化网格会选择六面体网格或者四面体网格，这些网格的表面都是平面。如下图所示的六面体网格离散的岩芯模型:

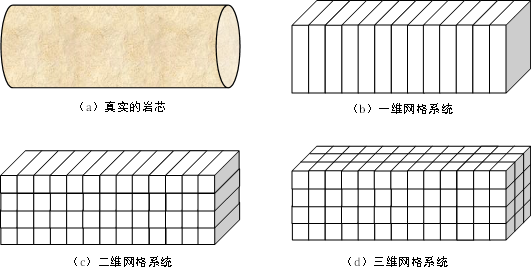
_images/rs007.png

在这里有人可能会提出疑问，这样离散成的网格系统跟原来的岩芯大不相同，原来是圆柱，现在就是一个个小矩形块组成的大矩形块而已。提出这样的问题很正常，这个问题也是我们在做数值模拟中一定要弄清楚而且熟记于心的问题，就是数值模拟中，研究目的决定了手段和结果。

首先，对于岩芯模拟这个问题，我们研究的目的是得到不同时刻岩芯中的流量、饱和度、压力的变化，这些才是最重要的。而需要计算出这些变化动态，只要能把岩芯的物理性质、横截面积、体积、流体物性等等特征模拟出来参与计算就可以了。至于数学模型内部用的岩芯是不是圆柱、有没有弧形边界都是不重要，对分析的结果影响可以忽略。其次，以目前的技术手段而言，使用曲面的网格在数学上不便于表达，会增加额外的负担，研究人员需要输入更多的参数，增加了使用的负担；计算机要处理更多的渲染计算，增加了处理计算的负担。就像三维游戏一样，一开始的物体也是由少数的多多面体构成的，看起来很粗糙。在几十年间计算机性能提高了以后，才逐步的出现了各种仿真系统，模拟复杂的表面、皮肤效果、天气效果等等。因此随着技术的发展，这些都可以能会应用到油藏数值模拟中，但是目前还有一定困难。因此在模拟计算时我们会选择简化的模型，而在使用简化模型计算出结果以后，可以选择开发出专门的三维显示软件来展示结果。此时的三维软件可以渲染得非常好，现有仿真显示技术已经可以做到以假乱真了。后面会涉及到油藏数值模拟软件的体系结构。这样的展示软件我们称为油藏数值模拟的“后处理”软件。

在离散化出网格系统后，每一个网格就是研究问题中的一个小单元，这个小单元跟之前推导公式过程中所指的控制体积有些类似。每一个网格我们会赋予一定的属性，这些属性包括以下几类：

（1）网格物理属性。就是把原来的真实物体的物理属性按照一定的算法分布到这些网格上。这样的属性包括孔隙度、渗透率这些属性参数，同样不要忘记网格本身的形状参数，网格内部的总孔隙体积要用总体积作为参考来计算。如果对于热采模型，还需要给出热容、导热系数等参数。

（2）流体的属性。这些属性包括流体的分布、饱和度、压力等等参数。由于是求解流体流动方程，所以流体的属性最为重要。

（3）源汇点的属性。如果是对于油藏的模型，有些网格会包括井的模型，有注入井（源点）和生产井（汇点）。这样网格就会含有井的属性，如井的形状参数、井内半径、表皮因子等等。有时网格中还可能包括额外的水体模型，水体模型可能是源点也可能是汇点。这样网格的属性就会有水体的压力、压缩系统等属性参数。

当真实模型的离散化网格系统建立好以后，对于每一个网格都对应一组流动方程。

2.1.2. 代数方程组的建立#

这样我们可以使用有限差分法来对流动方程进行处理。有限差分法的思路，就是找到有限个离散点，在这些离散点处求得原方程的近似表达式。然后我们用在这些离散点处的近似的表达式代替原来的微分方程，这些方程称为有限差分方程。经过有限差分法处理后的微分问题变成了代数问题，我们就可以用数值方法求解代数方程组来得到结果。我们用一维网格来说明这个过程。

_images/rs008.png

如上图所示，网格 \(x_i\) 与网格 \(x_{i-1}\) 及网格 \(x_{i+1}\) 是相邻网格，网格尺寸是均质的。流动会从一个网格的中心通过接触面流到另一个网格的中心。对于网格 \(x_i\) 来讲，由流体流动引起的变化量就是从网格 \(x_i\) 流到网格 \(x_{i-1}\) 的流量与从网格 \(x_i\) 流到网格 \(x_{i-1}\) 的流量之和。即通过网格面 \(x_{i-\frac{1}{2}}\) 和网格面 \(x_{i+\frac{1}{2}}\) 处的流量之和。以三相流动中的水相流动方程为例（如下式：）。

\[\nabla\cdot\left[\frac{kk_{rw}}{{B_w\mu}_w}\left(\nabla p_w+\rho_w\vec{g}\right)\right]=\frac{\partial}{\partial t}\left[\frac{1}{B_w}\phi S_w\right]+q_w\]

采用两点有限差分形式，对于任意一网格 \(i\) （位置在 \(x_i\) ），上述方程的左端变为如下有限差分表达式：

\[\nabla\cdot\left[\frac{kk_{rw}}{{B_w\mu}_w}\left(\nabla p_w+\rho_w\vec{g}\right)\right]\approx\sum_{j=1}^{n}f_{wj}=\sum_{j=1}^{n}T_{ij}\frac{k_{rw}}{{B_w\mu}_w}\Delta P_{w,ij}\]

其中：

  • \(j\) ，与网格i相邻并接触的任意网格；

  • \(n\) ，与网格i相邻并接触的网格个数；

  • \(f_{wj}\) ，从网格j流入网格i的流量；

  • \(T_{ij}\) ，与网格i与与网格j之间的网格传导率；

  • \(\Delta P_{w,ij}\) ，与网格i与与网格j之间的水相压力差，即 \(\Delta P_{w,ij}=P_{wj}-P_{wi}\)。

水相流动方程中的累积项需要进行时间差分，考虑到从时间 \(t\) 经过 \(\Delta t\) 时间后到 \(t+\Delta t\) 时间的累积项的表达式为：

\[\frac{\partial}{\partial t}\left[\frac{1}{B_w}\emptyset S_w\right]\approx\frac{\left[V_{pore}\frac{S_w}{B_w}\right]^{t+\Delta t}-\left[V_{pore}\frac{S_w}{B_w}\right]^t}{\Delta t}\]

其中： - \(V_{pore}\) ，是不同时刻的孔隙体积。

为了保持推导过程简要，源汇项任然保持流量的表达形式，只是考虑多个源汇点存在将源汇项做如下处理：

\[q_w=\sum_{k=1}^{m}q_w^k\]

其中：

  • \(m\) ，是网格 \(i\) 中源汇项的个数；

  • \(q_w^k\) ，是网格 \(i\) 中任意一个源汇项 \(k\) 的流量；

于是我们得到了水相流动方程的有限差分表达形式：

\[{\small F_{wi}=\sum_{j=1}^{n}T_{ij}\frac{k_{rw}}{{B_w\mu}_w}\Delta P_{w,ij}+\frac{\left[V_{pore}\frac{S_w}{B_w}\right]^{t+\Delta t}-\left[V_{pore}\frac{S_w}{B_w}\right]^t}{\Delta t}+\sum_{k=1}^{m}q_w^k }\]

实际上述方程在有限差分过程中会包含余项，也叫局部离散误差。为了简化本处省略该项。与水相类似，我们可以得到油相与气相的流动方程的有限差分表达形式为：

\[{\small F_{oi}=\sum_{j=1}^{n}T_{ij}\left(\frac{k_{ro}}{{B_o\mu}_o}+\frac{R_vk_{rg}}{{B_g\mu}_g}\right)\Delta P_{o,ij}+\frac{\left[V_{pore}\left(\frac{S_o}{B_o}+\frac{R_vS_g}{B_g}\right)\right]^{t+\Delta t}-\left[V_{pore}\left(\frac{S_o}{B_o}+\frac{R_vS_g}{B_g}\right)\right]^t}{\Delta t}+\sum_{k=1}^{m}q_o^k }\]

其中：

\[\sum_{k=1}^{m}q_o^k=\sum_{k=1}^{m}\left(q_{fo}^k+q_g^k\cdot R_v^k\right)\]

同理可得气相的流动方程的有限差分表达形式为：

\[{\small F_{gi}=\sum_{j=1}^{n}T_{ij}\left(\frac{k_{rg}}{{B_g\mu}_g}+\frac{R_sk_{ro}}{{B_o\mu}_o}\right)\Delta P_{g,ij}+\frac{\left[V_{pore}\left(\frac{S_g}{B_g}+\frac{R_sS_o}{B_o}\right)\right]^{t+\Delta t}-\left[V_{pore}\left(\frac{S_g}{B_g}+\frac{R_sS_o}{B_o}\right)\right]^t}{\Delta t}+\sum_{k=1}^{m}q_g^k }\]

其中：

\[\sum_{k=1}^{m}q_g^k=\sum_{k=1}^{m}\left(q_{fg}^k+q_o^k\cdot R_s^k\right)\]

对于三相黑油模型来说，对于每个网格i，上述方程的未知数有三个：

\[\begin{split}\mathbin{X}_i^{t+\Delta t}=\left[\begin{matrix}P_o\\S_w\\R_g\\\end{matrix}\right]_i^{t+\Delta t}\end{split}\]

其中：

  • \(t+\Delta t\) ，此上标表示当前时间步的值，是未知数，前一个时间步的变量都用 \(t\) 上标标注，是已知的；

  • \(R_g\) ，在不同条件下可以是 \(S_{gi}\) 、 \(R_s`或 :math:`R_{vi}\) 中的任意一个。取决于油气两相之间的相平衡状态。

假如我们建立了N个网格的离散化网格系统，每个网格有油气水三个流动方程，最终我们得到了3N个方程所组成的非线性方程组。这个方程组有3N个未知数。为了便于后面介绍该非线性方程组的解法，我们把方程组可以用如下符号表示：

\[\mathbin{F}\left(\mathbin{X}^{t+\Delta t}\right)=\mathbin{F}\left(\mathbin{P}_o^{t+\Delta t},\mathbin{S}_w^{t+\Delta t},\mathbin{R}_g^{t+\Delta t}\right)=0\]

这里我们不再赘述这个方程组的误差以及是否有解的条件。有兴趣的读者可以参考相关资料。

2.1.3. 非线性方程组求解#

对于前面得到的有限差分方程组，有不同的方法可以求解。例如全隐式方法（简称FULLIMP方法）、隐压显饱方法（简称IMPES方法）、自适应显隐方法（简称AIM方法）来求解。FULLIMP方法就是求解式时所有未知数在当前时间步同时求解，这个也是黑油模型油藏数值模拟的默认解法，适合求解相对复杂的实际问题。而IMPES就是先把压力作为未知数，此时假设由饱和度引起的值在求解压力时不发生变化，因此和当前时间步的饱和度相关的值比如毛管力保持不变。这样先求出压力值以后，再重新显示计算出饱和度和其他与饱和度相关值。我们以油水两相的方程组来说明一下IMPES方法的过程。两相的方程组按照上一小节末的介绍可以表示如下：

\[\mathbin{F}\left(\mathbin{P}_o^{t+\Delta t},\mathbin{S}_w^{t+\Delta t}\right)=0\]

采用IMPES方法时，第一步假设饱和度相关的参数不变化。含水饱和度 \(\mathbin{S}_w^{t+\Delta t}\) 使用上一个时间步的值 \(\mathbin{S}_w^t\) ，这样方程就变为：

\[\left.\mathbin{F}\left(\mathbin{P}_o^{t+\Delta t}\right)\right|_{\mathbin{S}_w^{t+\Delta t}=\mathbin{S}_w^t}=0\]

注意此时方程未知数减少了，所以计算量相应减少了。求解上述的简化后的非线性方程组，得到压力未知数 \(\mathbin{P}_o^{t+\Delta t}\) 后，再用压力值和饱和度的公式直接计算出 \(\mathbin{S}_w^{t+\Delta t}\) 。

FULLIMP方法的优点是稳定性好，但是缺点是计算量大，速度比IMPES方法慢。而IMPES方法的优点是求解线性方程组要小，计算比FULLIMP方法要快很多，而缺点是因为饱和度未知数是显示计算，稳定性差， \(\Delta t\) 不能太大。AIM方法顾名思义就是设置一定的条件，满足这些条件的网格采用FULLIMP方法，而其他网格采用IMPES方法，由于各种参数是在动态变化的，所以满足条件的网格也是动态变化的，所以叫做自适应显隐方法。

这里我们重点介绍一下FULLIMP方法的求解细节。现代油藏数值模拟中FULLIMP方法主要求解思路是使用牛顿迭代法。牛顿迭代法又叫做牛顿下山法，这种叫法是一种很形象的比喻。我们先看一个一元函数方程使用牛顿迭代法的求解过程。令：

\[f\left(x\right)=0\]

下面开始求解的迭代流程。

（1）过初值点 \(x_i\) 做 \(f\left(x\right)\) 切线 \(L_i\) ，该切线方程如下：

\[y=f\left(x_i\right)+f^\prime\left(x_i\right)\left(x-x_i\right)\]

（2）求出该切线与X轴的交点的 \(x\) 值即 \(x_{i+1}\) ；

（3）如 \(x_{i+1}\) 满足迭代收敛条件，则 \(x_{i+1}\) 即为方程的解；否则令 \(x_{i+1}\) 作为迭代初值，重复步骤（1）~（3）。

迭代收敛条件有不同的计算方式，可以直接计算 \(f\left(x_{i+1}\right)\) 的值，如果这个值的绝对值小于一个极小值即 \(f\left(x_{i+1}\right)\le\varepsilon_{min}\approx0\) ，那么可以认为 \(x_{i+1}\) 使方程成立。也可以有一些其他方式，例如计算如 \(x_{i+1}\) 并计算 \(x_i\) 与 \(x_{i+1}\) 之间的变化量，可以用下述的相对误差量来计算：

\[\varepsilon=\left|\frac{x_i-x_{i+1}}{x_i}\right|\]

如果 \(\varepsilon\) 小于一个极小值 \(\varepsilon_{lim}\) ，说明两次迭代的解之间几乎无变化，迭代达到一个极限条件，再次迭代也无意义，这个作为一个收敛条件，也可以退出迭代。我们用下图来模拟上述的过程：

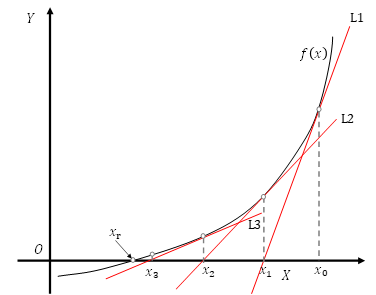
_images/rs009.png

假设 \(x_r\) 是上述方程的解，我们选择 \(x_0\) 作为方程的初始解， \(x_0\) 可能接近 \(x_r\) ，也可能两者相差很远。通常情况下，如果 \(x_0\) 接近 \(x_r\) ，牛顿迭代法有非常快的收敛速度。从上述过程可以推导出牛顿迭代法的迭代表达式如下：

\[x_{i+1}=x_i-\frac{f\left(x_i\right)}{f^\prime\left(x_i\right)}\]

可以认为通过上述迭代公式，可以利用函数及其导数可以从任意当前值 \(x_i\) 计算出逼近真实解的增量 \(\delta x\) ，如下：

\[\delta x=-\frac{f\left(x_i\right)}{f^\prime\left(x_i\right)}\]

我们把上述牛顿迭代法应用于求解前面的油水两相模型所得到的流动方程的方程组。该方程组的未知数的迭代表达式为：

\[\mathbin{X}_{i+1}=\mathbin{X}_i+\left({\mathbin{Jac}}^{-1}\cdot-\mathbin{F}\left(\mathbin{X}_i\right)\right)\]

其中：

  • \(\mathbin{X}_i\) ，是当前迭代步 \(i\) 的未知数的初值；

  • \(\mathbin{Jac}\)，是 \(\mathbin{F}\left(\mathbin{X}\right)\) 的雅各比矩阵；是方程组对每一个变量求偏导数的矩阵；

  • \({\mathbin{Jac}}^{-1}\) ，是雅各比矩阵的逆矩阵；

  • \(\mathbin{X}_{i+1}\) ，是求解出的新未知数值，如果此时满足收敛条件，就是当前方程组的解；如果此时不满足收敛条件，就是下迭代步的初值。

因此未知数的增量 \(\delta\mathbin{X}\) 可以表示为：

\[\delta\mathbin{X}={\mathbin{Jac}}^{-1}\cdot-\mathbin{F}\left(\mathbin{X}_i\right)\]

实际上求矩阵的逆非常困难，因此上式可以转化为如下形式：

\[\mathbin{Jac}\cdot\ \delta\mathbin{X}=-\mathbin{F}\left(\mathbin{X}_i\right)\]

上述表达式是一个线性方程组，形如 \(\mathbin{AX}=\mathbin{B}\) 的形式。 \(\mathbin{Jac}\) 矩阵是一个 \(m⨯m\) 的稀疏矩阵，其形式由下图所示：

_images/rs010.png

而 \(\delta\mathbin{X}\) 和 \(-\mathbin{F}\left(\mathbin{X}_i\right)\) 都是一个m维的向量。于是可以选择使用合适的数值方法进行求解，得到 \(\delta\mathbin{X}\) ，进而求出新一次迭代的解 \(\mathbin{X}_{i+1}\) 。如果 \(\mathbin{F}\left(\mathbin{X}_{i+1}\right)\) 达到收敛条件，方程组就成功求解。否则就继续迭代，直到达到最大的收敛次数限制为止。此稀疏矩阵线性方程组的解法一般有GMRES方法、BICG方法等。

2.1.4. 收敛条件#

由于 \(\mathbin{F}\left(\mathbin{X}\right)\) 是流动方程的有限差分方程组，在判断收敛条件时，需要有一定的物理意义，不能像只是求解普通数学问题一样，求得一个数学解。这里我们考虑比较三相黑油模型得情况。对于有N个网格得模型， \(\mathbin{F}\left(\mathbin{X}\right)\) 是一个包含3N个非线性方程的方程组。其中，每个网格对应3个方程，三个方程分别对应的是油、水、气各相的流动方程。（提示读者参考哪个章节）。对于每个迭代步得到的 \(\mathbin{X}_{i+1}\) ，都可以求出 \(\mathbin{F}\left(\mathbin{X}_{i+1}\right)\) 。因此对于每一个网格j，可以定义代入解后的方程残差如下：

\[\begin{split}\left\{\begin{matrix} R_{wj}=F_w\left(X_j\right)=T_w\left(X_j\right)+{\delta M}_w\left(X_j\right)+Q_w\left(X_j\right)\\ R_{oj}=F_o\left(X_j\right)=T_o\left(X_j\right)+{\delta M}_o\left(X_j\right)+Q_o\left(X_j\right)\\ R_{gj}=F_g\left(X_j\right)=T_g\left(X_j\right)+{\delta M}_g\left(X_j\right)+Q_g\left(X_j\right) \end{matrix}\right.\end{split}\]

其中：

  • \(R_{wj}\)、 \(R_{oj}\)、 \(R_{gj}`分别是当前的解 :math:`X_j\) 代入方程组 \(F\left(X\right)\) 后得到的水、油、气方程所得到的残差残差；

  • \(T\left(X_j\right)\)，是方程的流量项；

  • \(\delta M\left(X_j\right)\)，是方程的累积项；

  • \(Q\left(X_j\right)\)，是方程源汇项。

整个方程组的残差表示如下:

\[\mathbin{R}=\mathbin{F}\left(\mathbin{X}_{i+1}\right)\]

如果上述的残差项 \(\mathbin{R}\) 足够小，就说明 \(\mathbin{F}\left(\mathbin{X}_{i+1}\right)\) 满足精度要求， \(\mathbin{X}_{i+1}\) 是当前时间步的解。在油藏数值模拟中，我们使用了质量守恒定律，因此可以建立残差和油藏孔隙体积的关系，进行比较来衡量残差的大小。因此建立如下的物质平衡误差公式：

\[E=\ \frac{\sum_{j=1}^{n}\left(R_j\right)}{\sum_{j=1}^{n}\left(V_j\right)}\cdot∆t\cdot\widetilde{B}\]

其中：

  • \(E\) ，被物质平衡误差；

  • \(n\) ，网格个数；

  • \(\bar{B}\) ，平均体积系数；

  • \(V_j\) ，每个网格的孔隙体积；

  • \(R_j\) ，每个网格的残差值。

由于残差项是流量项，是体积速率，残差项乘以时间 \(∆t\) ，转换成体积值，然后乘以体积系数，转换为地下条件的体积，最后和孔隙体积进行比较，如果 \(E\) 的值小于一个极小值 \(E_{min}\) ，那么就认为残差满足精度要求。在实际的实现中，由于地下分为多个相，为了避免各相的绝对值相差较大互相影响，应对不同的相分别利用上述公式计算物质平衡误差。即分别求出水、油、气各相的物质平衡误差 \(E_w\) 、 \(E_o\) 、 \(E_g\) ，当各相的物质平衡误差都同时小于 \(E_{min}\) 才能认为方程组达到精度要求条件。 \(E_{min}\) 的取值一般是 \(10^{-6}\) 。

实际的数值计算结果已经告诉我们，大多数情况下，所求得的物质平衡误差往往都比较小，即物质平衡误差很容易达到要求。有一部分原因是因为在上述公式求和的时候，有的残差可能数值的绝对值较大，但是这些数值之间，正负相加后被互相抵消，因此最后的结果数值比较小。因此为了保证数值结果的精度，往往还需要考察残差的绝对值，即增加一个额外的收敛条件。如下述公式所示：

\[E_{non}=\ max\left(\left|\frac{R_j}{V_j}\right|\right)\cdot∆t\cdot\widetilde{B}\]

上式中 \(E_{non}\) 是残差值与孔隙体积之比的绝对值最大的数计算得到的。如果这个值也能小于一个界限值，那么就可以说明整体的方程组残差跟其自身的所表示网格的孔隙体积之比都较小，符合数值计算的精度要求。上述公式也需要分别对油水气各相进行计算。 \(E_{non}\) 满足精度条件的上限制一般取 \(10^{-3}\) ，即0.001。