时间步大小的影响#

油藏数值模拟计算包含了大量数值计算过程，这些过程被编成程序代码在计算机上运算。而计算机的浮点数运算中不可避免的会受到截断误差的影响。这个影响是不能被忽略的，任何使用油藏数值模拟器的用户、编写数值模拟算法代码的开发者、测试油藏数值模拟功能的测试人员等，都需要重视这个问题。

为了让大家容易理解这个问题，我们可以用一个例子来说明这个影响。假设我们有一个油藏，生产了3500天，我们创建了一个模型来表征这个油藏。假设我们每次算100天，一共需要35次。如果每次算5天，就需要700次。由于截断误差所带来的影响，虽然这两种情况最后都模拟了3500天，每次迭代计算都符合精度要求，但是它们最后的结果可能会差别很大，有时候的相对误差会超过50%，甚至更高。

如果上面的误差情况是真实存在的，那么这就可以回答很多人关心的一个问题”同一个模拟器，同一个模型，是不是计算出的结果一致？“。很遗憾的是，这个误差是真实存在的。我们可以创建一个上述模型的算例来测试一下。

测试模型#

我们创建一个40x40x3的模型，模型的属性分布为均质分布。其实可以创建一个单层模型，但是为了跟实际油藏模型更接近，模型纵向分3个K层。

../_images/diffts_grid_depth.png

模型的网格图（属性为深度） [1]#

重要

  • 如果没有特殊说明，本章的模型均由cFlow模拟器计算。

  • 点击 下载数据体 (SHA1: b45131f9c294af5eb89c5b4059bab5df050d04ff)。

基于相同一个模型，我们采用不同的计算时间步进行计算。3500天分为35个报告步，每个报告步100天。C1模型的最大时间步限制为100天，跟报告步长度一致，也就是说在报告步之内不限制时间步的长度。C2模型的最大时间步限制为5天，即每计算一个报告步100天，至少需要20次才能算完。C3模型的最大时间步限制为30天，也就是每个报告步100天至少需要算4次才能算完。下表做了一个汇总。

../_images/diffts_model_setting.png

三个模型的设置#

计算结果#

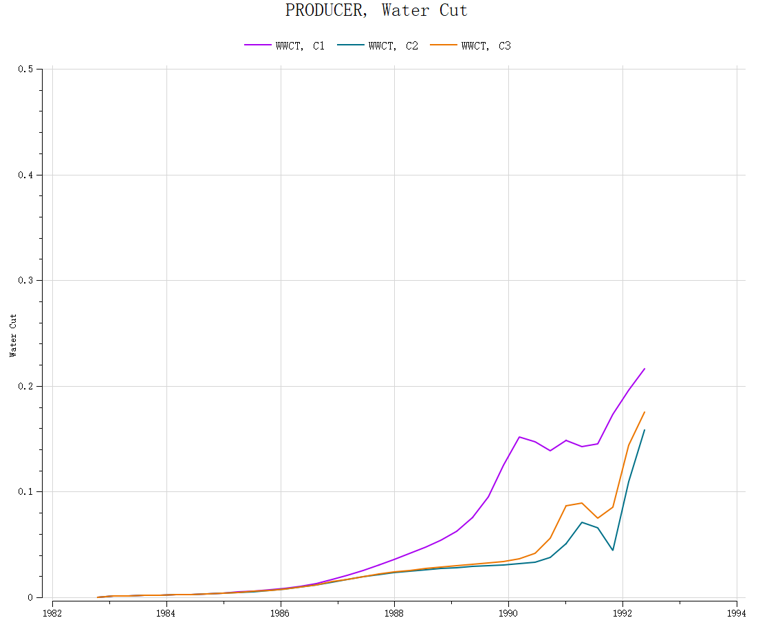
cFlow模拟器计算这三个模型几乎没有收敛性问题，计算完成后将三个模型的含水率曲线进行对比，如下图：

../_images/diffts_wwct_all.png

三个模型计算后的含水率曲线 [1]#

重要

不同的模拟器可能由于设置不同会可能出现收敛性问题，但是结果不会受影响。因为模拟器在遇到收敛性问题时，都会减小时间步来处理，所以计算时间步不会超过设置，计算出的结果可以用于对比。

从对比结果很明显的就可以看到，后期的含水率曲线误差较大，最大的地方已经模型间的相对误差已经超过了100%。这些误差就是在不同计算时间步控制影响后的结果。在这个例子中，结果有误差并不是最大的影响。如果仔细观察，可以看到在1992年之前附近的一段时间，三个模型的规律不一致。C1模型和C3模型的含水率是上升的，而C2模型的含水率是下降的。

获取测试模型#

点后面链接下载 测试模型 。

备注

上述几个模型如果用其它模拟器计算也会有相同的结果。

进一步探索底层#

类似这样的模型还有很多，比它复杂的模型更多，都可以充分的证明即便是同一个模拟器，如果计算时间步不同——即会导致实际的计算中的变量变化、数值处理过程不同——结果就可能会有明显的差异。到这里很多细心的读者会提出一个问题，那么如果不同的模拟器在计算同一个模型时，如果速度不同或收敛性不同都会导致时间步不同，这样也会产生误差吧？答案是肯定的。如果同一个模型，模拟器A效率高收敛性好，计算了2个小时，而模拟器B效率低且收敛性差，计算了2天甚至更长时间，它们的结果很可能出现较大差异，此时要比较或者强调A 和B的一致性是没有意义的。

数值计算的问题#

看到这里很多人已经明白造成这些误差的原因，那就是截断误差。对于一部分不太了解的读者，我们先来解释一下截断误差。这里我们需要说明一下计算机中的数值表示。计算机的底层是大量的开关电路，形象一点就是众多的0和1，它将连续的数值与离散的状态联系起来，使得我们可以近似真实世界的东西，但是这也有它的局限性。例如，在真实世界中我们可以写 \(\sqrt2\) ，但是在计算机中我们很难对sqrt2进行描述，在计算时它必须表示为具体的数值。众所周知， \(\sqrt2\) 是一个无理数，它的值为1.4142135623730950488016887242097……，小数点的后面是无穷多个数字。那么能不能用1.414或者1.41421356237来描述 \(\sqrt2\) 呢？下表对比了不同类型下 \(\sqrt2\) 的值。

数值类型

\(\sqrt2\) 的值

实际值

1.4142135623730950488016887242097……

单精度

1.414214

双精度

1.4142135623731

从上表可以看出，无论在用单精度还是双精度来代替 \(\sqrt2\) 进行数值计算，从某种程度上都是对其实际值进行了截断，这种利用有限项来近似无穷项所产生的误差，就称为截断误差。它在数值计算中无处不在，如简单的加减乘除、复杂积分或微分等等。可以说，截断误差是数值计算中造成数值结果与真实结果差别的主要原因。

亲自计算一个例子#

看到这里很多人会提出，用尽量多的有效位数来可以解决这个问题，避免截断或者减轻它的影响。例如使用64位或者更高的位数。这样固然可以增加精度，但是会增加数据项长度，在数值计算时不仅会占用更多内存空间而且会增加单个数据的操作时间，这些成本都需要考虑进去。更重要的是截断误差的影响往往伴随着不同的计算过程发生，这些过程并不因使用更多的有效位数而发生改变。为了说明这个问题，我们来计算下面的一个简单公式:

\[f\left(x\right)=\frac{1}{\sqrt{1+x}-\sqrt{1-x}}\]

在数模计算中所用到的公式可能比这个要复杂很多，同时我们也会遇到很多小的数值，例如刚刚脱气网格的含气饱和度、水刚刚可以流动时的相渗值以及其他很多的中间结果等等。这里我们x取双精度类型，当x取不同值时计算 \(f\left(x\right)\) 值。同时我们用另外一种方法来计算 \(f\left(x\right)\) 并与原式比较结果，将 \(f\left(x\right)\) 进行如下变形得到新的函数 \(g\left(x\right)\) :

\[g\left(x\right)=\frac{1}{\sqrt{1+x}-\sqrt{1-x}}\times\frac{\sqrt{1+x}+\sqrt{1-x}}{\sqrt{1+x}+\sqrt{1-x}}=\frac{\sqrt{1+x}+\sqrt{1-x}}{2x}\]

上面两个表达式 \(g\left(x\right)\) 与 \(f\left(x\right)\) 是相等的。取不同的 \(x\) 值计算后得到下表（注：下表在Excel2016的Visual Basic中计算， \(x\) 定义为double类型）：

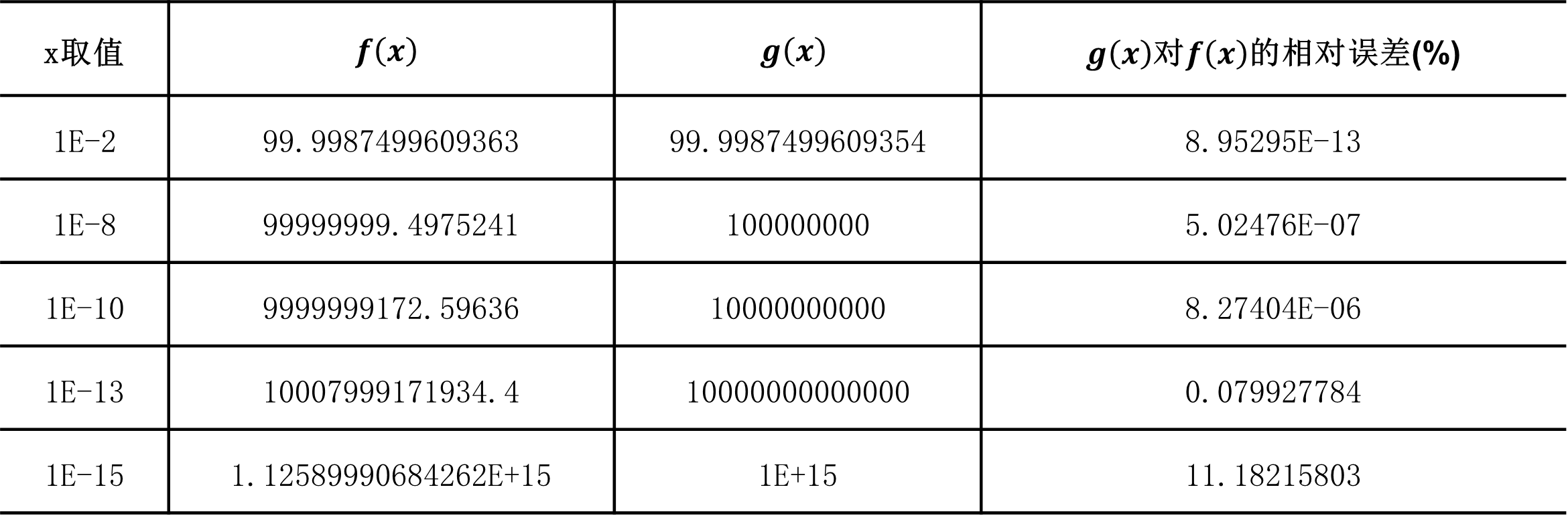
../_images/diffts_calc_res01.png

两个公式的计算结果对比#

从计算结果可以看出，在x在取较小值的的时候，两种方法计算出的结果误差逐渐变得显著。一部分读者可能已经指出变形 \(g\left(x\right)\) 才是比原式更理想的计算方法（由于篇幅关系不深入讨论，请读者自行查阅相关资料），可以认为变形 \(g\left(x\right)\) 后计算的结果更接近真实世界，而直接用原式计算 \(f\left(x\right)\) 反而与结果在 \(x\) 较小时产生很大误差，这是增大有效位数无法解决的误差问题。相同的公式如果用不同的算法来求解，可能会得到不一样的而结果，不好的算法得到错误的结果。

不敢想象如果这些发生在油藏数值模拟的计算中，将会产生怎样不可思议的结果。但是这些情况确实一直在油藏数值模拟中发生，不同的计算过程再加上计算机的“截断”过程造就了这些误差。庆幸的是很多的科学家都在不断的改进算法来求解数学模型，使得这个影响逐步降低，例如本例对 \(f\left(x\right)\) 的变形处理。很多时候一些数学方程在经过算法改造后，可以更容易收敛。这也就是为什么说光靠理论公式形成不了好的模拟器软件，因为大量的公式需要有合适的算法来实现，如果算法实现得有问题，引起数值计算的阶段误差累积太大，就会导致计算不稳定，要么出现不合理的结果，要么计算缓慢不收敛。

重要

在用油藏数值模拟进行预测时，往往预测时间段越长结果可能越不准确，因为在预测阶段的后期，每个报告步的长度可能是一个季度后者半年甚至是1年，如果不限制计算时间步，一般模拟器可能会默认限制为100天，这样长的时间步计算的结果和按月（即30天）计算的时间步的结果可能有很大误差，所以越是预测后期，所计算的结果不确定性越高；要想提高准确度的办法就是使用较小的计算时间步，如以月为单位。

小结#

综合上述的两个例子，从某个具体公式的算法，到集合大量公式算法的模拟器算法，都需要考虑减少算法的精度和稳定性。同时，我们在油藏数值模拟中要正视造成这些误差的原因，如不同的解法、不同的时间步、采用并行计算等都会引起这些误差。于是收敛性差计算慢的模型会产生更多的误差，对于这样的模型要先尝试解决其收敛性问题，有时需要对数模数据体的一些错误数据进行适当修正；对于修正了问题但是收敛仍然很慢的情况，说明当前模拟器对模型的求解效率降低，则需要使用采用新算法新架构的模拟器来计算，否则花了大量时间勉强计算出的结果通常是误差较大的无效结果。

该图用ResInsight绘制。